Euler's column theory and slenderness ratio of column.

 ◼️ Euler's column theory:

        The first rational attempt, to study the stability of long columns, was made by Mr. Euler. He derived an equation, for the buckling load of long columns based on the bending stress. While deriving this equation, the effect of direct stress is neglected. This may be justified with the statement that the direct stress induced in a long column is negligible as compared to the bending stress. It may be noted that the Euler's formula cannot be used in the case of short columns, because the direct stress is considerable and hence cannot be neglected.

◼️Assumptions in the Euler's column theory:

      The following simplifying assumptions are made in the Euler's column theory:

1. Initially the column is perfectly straight and the load applied is truly axial.
2. The cross-sectional of the column is uniform throughout it's length.
3. The column material is perfectly elastic, homogeneous and isotropic and thus obeys Hooke's law.
4. The length of column is very large as compared to it's cross-sectional dimensions.
5. The shortening of column, due to direct comparison (being very small) is neglected.
6. The failure of column occurs due to buckling alone.

◼️Sign conventions:

     Through there are different signs used for the bending of columns in different books, yet we shall follow the following sign conventions which are commonly used and international recognised.

1. A moment, which tends to bend the column with convexity towards it's initial central line as shown in Fig. (a) is taken as positive.
2. A moment, which tends to bend the column with it's concavity towards it's initial central line as shown in Fig. (b) is taken as negative

◼️ Euler's formula and equivalent length of a column:

      In the previous article, we have derived the relation for the crippling load under various end conditions. Sometimes, all these cases are represented by a general equation called Euler's formula,

     Where Le is the equivalent or effective length of column.

      The is another way of representing the equation, for the crippling load by an equivalent length of effective length of a column. The equivalent length of a given column with given end conditions, is the length of an equivalent column of the same material and cross-sectional with both ends hinged and having the value of the crippling load equal to that of the given column.

      The equivalent lengths (L) for the given end conditions are given below:

◼️Limitation of Euler's formula:

     Euler's formula for the crippling load,

：· Euler's crippling stress, 

    A little consideration will show that the crippling stress will be high, when the slenderness ratio is small. We know that more than the crushing stress of the column material. It is this obvious that the Euler's formula will give the value of crippling stress of the column (equal to the crushing stress of the column material) corresponding to the slenderness ratio. Now consider a mild steel column. We know that the crushing stress for the mild steel is 320 MPa or 320 N/m² and Young's modulus for the mild steel is 209 GPa or 200×10³ N/mm². 

     Now equation the crippling stress to the crushing stress,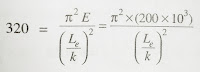

   Thus, if the slenderness ratio is less than 80 the Euler's formula for mild steel column is not valid.

    Sometimes, the columns, whose slenderness ratio is more than 80 are known as long columns and those whose whose slenderness ratio is less than 80 are known as short columns. It is thus obvious that the Euler's formula holds good only columns.

Note. In the Euler's formula, for crippling load, we have not taken into account the direct stresses induced in the material due to the load, (which increases gradually from zero to it's crippling value). As a matter of fact the combined stress, due to direct load and slight bending reaches it's allowable value at a load, lower than required for buckling; and therefore this will be limiting value of the safe load.

◼️Slenderness ratio:

     We have already discussed in this article that the Euler's formula for the crippling load, 

 ......(i)

    We know that the buckling of a column under the crippling load will take place about the axis of least resistance. Now substituting l= Ak² ( where A is the area and k is the least radius of gyration of the section) in the above equation,

......(ii)

    Where Le/k is known as slenderness ratio. The slenderness ratio is defined as ratio of equivalent (or unsupported) length of column to the least radius of gyration of the section.

Slenderness ratio dose not have any units.

******************************************

Thanks for watching and stay cool for more updates.

If you think this article has helped you, so please like, comment and share.

Official YouTube channel : Click to subscribe